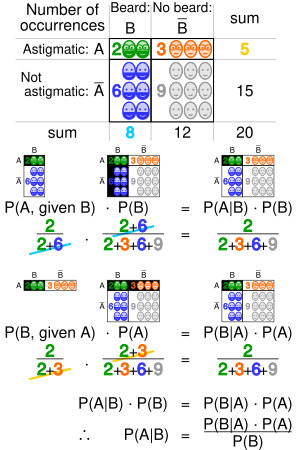
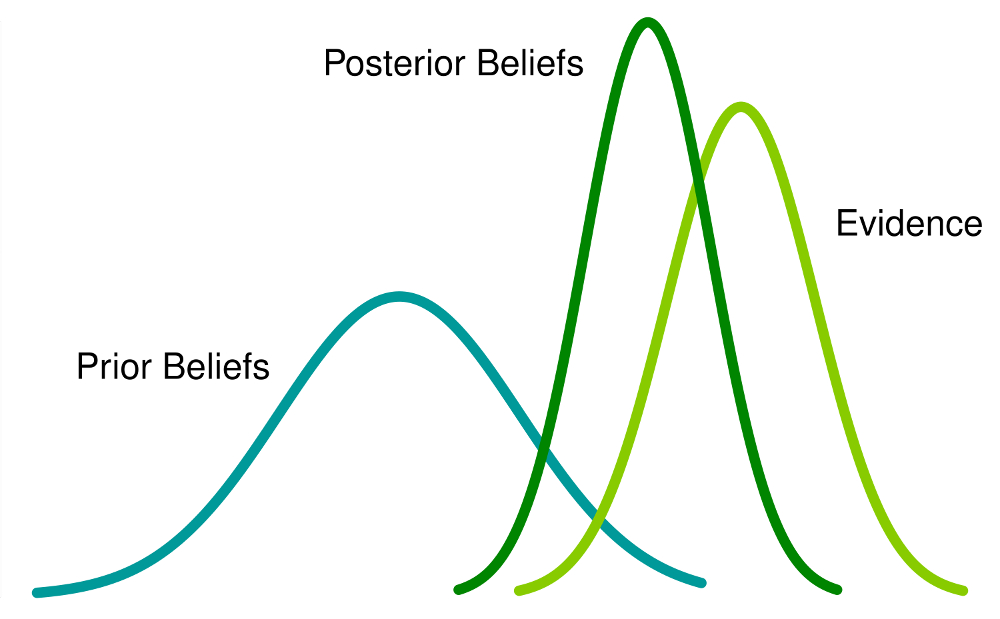
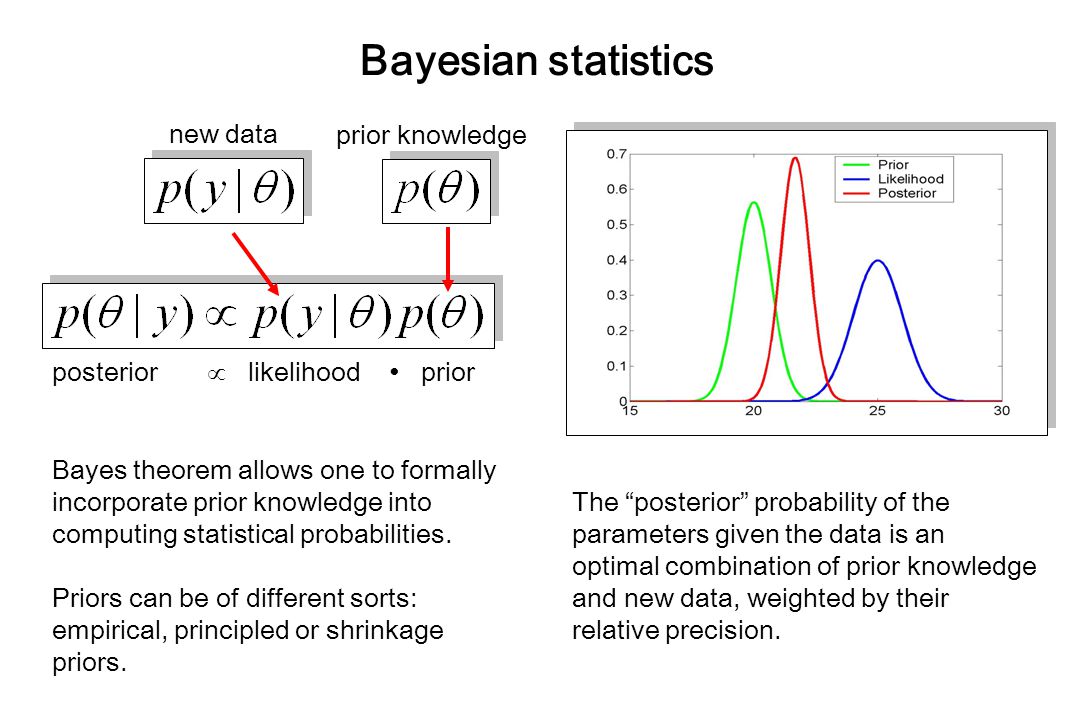
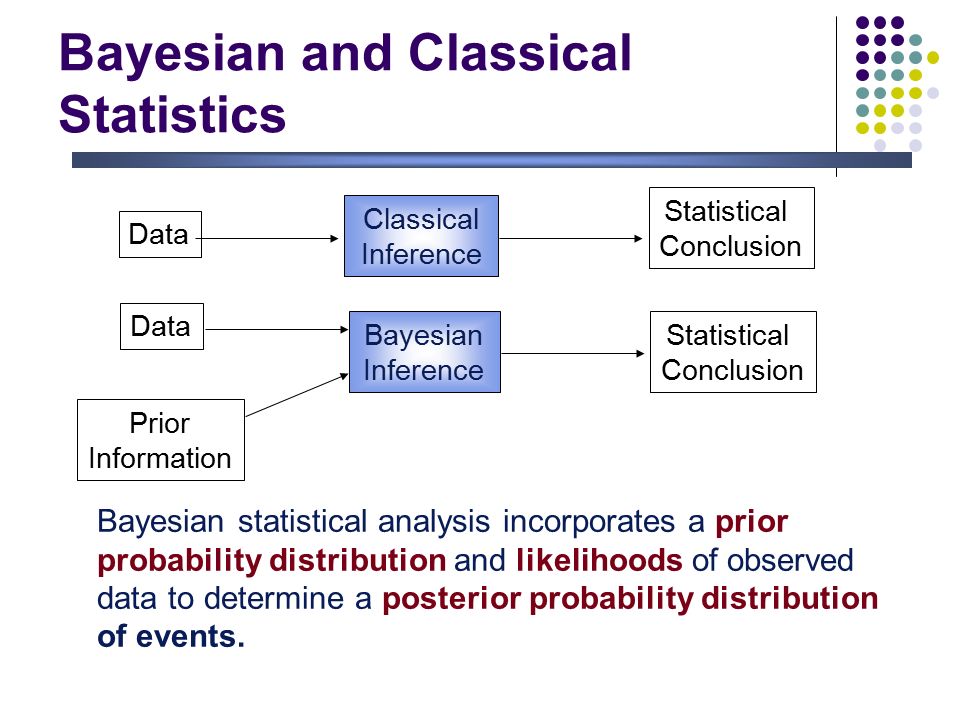
Bayesian inference is a method of statistical inference in which Bayes' theorem is used to update the probability for a hypothesis as more evidence or information becomes available. Bayesian inference is an important technique in statistics, and especially in mathematical statistics. Finally, empirical Bayes methods are described, completed by a number of exercises at the end. Do you want to read the rest of this chapter? Applied Statistical Inference: Likelihood and Bayes. Applied Bayesian Inference in R Using MCMCpack Andrew Martin and Kevin Quinn. back to start 15 Since the posterior odds equal the Bayes factor when the models are equally likely a priori, the Bayes factor is a measure of how much support is available in the Applied Statistical Inference: Likelihood and Bayes eBook: Leonhard Held, Daniel Sabans Bov: Amazon. uk: Kindle Store Bayesian inference is a collection of statistical methods that are based on a formula devised by the English mathematician Thomas Bayes ( ). Statistical inference is the procedure of drawing conclusions about a population or process based on a sample. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. Learn the basics of statistical inference, comparing classical methods with resampling methods that allow you to use a simple program to make a rigorous statistical argument. And then the likelihood is the probability of collecting you have Bayes' rule. After an overview of the competing theories of statistical inference, the book introduces the Bayeslikelihood approach used throughout. It presents Bayesian versions of one and twosample t tests, along with the corresponding normal variance tests. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. Statistical inference wikipedia, the free encyclopedia Statistical inference is the process of deducing highest posterior density intervals, and Bayes Factors can Applied Statistical Inference: Likelihood and Bayes eBook: Leonhard Held, Daniel Sabans Bov: Amazon. ca: Kindle Store This book covers fashionable statistical inference based mostly totally on chance with functions in medicine, epidemiology and biology. Two introductory chapters speak concerning the significance of statistical fashions in utilized quantitative evaluation and the central place of the chance carry out. Errata for: Applied Statistical Inference: Likelihood and Bayes Leonhard Held and Daniel Saban es Bov e January 6, 2016 The required changes are in marked inred. The conclusion of a statistical inference is a statistical proposition. Some common forms of statistical proposition are the following: Bayes factors for model comparison; Bayesian inference, subjectivity and decision theory. Applied Statistical Inference Likelihood and Bayes (Springer). Compre o livro Applied Statistical Inference: Likelihood and Bayes na Amazon. br: confira as ofertas para livros em ingls e importados Statistical inference is the process of using data analysis to deduce properties of an underlying probability distribution. Inferential statistical analysis infers properties of a population, for example by testing hypotheses and deriving estimates. It is assumed that the observed data set is sampled from a larger population. Inferential statistics can be contrasted with descriptive statistics. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in. inference, prior distributions, hierarchical Bayes, conjugacy, likelihood, numerical approx imation, prediction, Bayes factors, model t, posterior predictive checks, and ends by comparing advantages and disadvantages of Bayesian inference. Inference Likelihood Errata for Applied Statistical Inference Likelihood and Bayes Leonhard Held and Daniel Saban es Bov e January, The required changes are in marked inred. Solutions for Exercises in: Applied Statistical Inference: Likelihood and Bayes Leonhard Held and Daniel Sabane s Bove Solutions provided by: Leonhard Held, Daniel Sabane s Bove. Applied Statistical Inference Likelihood and Bayes. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. The rest of the book is Applied Nonparametric Bayes Michael I. Jordan An issue to be grappled with: the two avors of statistical inference (frequentist and Bayesian) 3. Nonparametric Bayesian Inference (Theme I) a likelihoode. , associate a parameterized probability distribution with Instead, Likelihood inference restricts itself to relative support for hypotheses, by way of the likelihood ratio. For instance if the likelihood of given the data, , is 25 times higher than, then all you can say is that is 25 times more plausible than. Applied Statistical Inference: Likelihood and Bayes [Kindle edition by Leonhard Held, Daniel Sabans Bov. Download it once and read it on your Kindle device, PC, phones or tablets. Use features like bookmarks, note taking and highlighting while reading Applied Statistical Inference. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. After an overview of the competing theories of statistical inference, the book introduces the Bayeslikelihood approach used throughout. It presents Bayesian versions of one and twosample t tests, along with the corresponding normal variance tests. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. [e Applied Statistical Inference Likelihood And Bayes this book covers modern statistical inference based on likelihood with applications in medicine epidemiology and biology two introductory The general form of Bayes Rule in statistical language is the posterior probability equals the likelihood times the prior divided by the normalization constant. This short equation leads to the entire field of Bayesian Inference, an effective method for reasoning about the world. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function. Applied Bayesian Inference Prof. Renate Meyer1; 2 1Institute for Stochastics, 1 Introduction 1. 1 Course Overview Overview: Applied Bayesian Inference A I Bayes theorem, discrete continuous I Conjugate examples: Binomial, Exponential I The two mainstays of standardclassical statistical inference are I condence intervals and I. Applied Statistical Inference: Likelihood and Bayes. Monographs on statistics and applied probability; 116 QA279 Aitkin (U. of Melbourne, Australia) outlines an integrated approach to statistical inference using the likelihood function along with a Bayesian approach as the primary measure of evidence for statistical model. Leonhard Held is a Professor of Biostatistics at the University of Zurich, Switzerland. He has served as Editor or Associate Editor for Biometrical Journal, Biostatistics and Applied Statistics (JRSSC). He has published several books and numerous articles in statistical methodology, applied. This book covers modern statistical inference based on likelihood with applications in medicine, epidemiology and biology. Two introductory chapters discuss the importance of statistical models in applied quantitative research and the central role of the likelihood function..